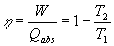Bem, temos um problema na mão que incomoda qualquer engenheiro que queira fazer uma máquina ou um motor funcionar com rendimento grande. Entenda grande como próximo a 100%.
Antes de mais nada, a natureza não nos permite que ao introduzir energia em uma máquina, essa energia seja toda convertida em trabalho. Vejam bem, vejam bem! Quando introduzimos energia em qualquer objeto da natureza, parte dessa energia é transformada em energia interna (U). A energia interna, do ponto de vista micro da matéria, é a soma das energias potenciais e cinéticas das partículas que formam o corpo. Com isso, afirmo que só existe, na natureza, estas duas formas de energia. As outras, não passam de visão macro das mesmas.
Bem, após essa consideração, vamos a questão:
Já que uma máquina térmica não converte toda energia recebida em trabalho, Carnot propôs que uma máquina funcionará com rendimento máximo se estiver entre duas isobáricas e duas isotermas, como mostra a figura:
Um motor que funcione nesse ciclo, segundo Carnot, terá o maior rendimento. Ele precisa funcionar entre as temperaturas Ta e Tb, duas isotermas, e as duas adiabáticas ad e bc.
Este gráfico nos informa que quando a energia Qa entra no sistema pela isoterma Ta, ela realiza trabalho (W) e outra parte é absorvida pelo sistema na forma de energia interna U. Se essa energia interna não for jogada para fora, nosso sistema, ou motor, derreterá após aumentar sua temperatura. Portanto, ela é jogada para fora na isoterma Tb, representada pela quantidade de energia Qb. Assim, vemos que para fechar o ciclo, precisamos injetar energia Qa que realiza trabalho e aumenta a energia interna do sistema que é jogada para fora na forma de Qb.
A equação abaixo, nos informa que o rendimento de uma máquina nunca pode ser 100% pois a temperatura 2 (ou Tb) é menor que a temperatura 1 (ou Ta). A temperatura 2 é a temperatura da fonte "fria" e a temperatura 1 é da fonte "quente". Portanto, a divisão da temperatura 2 pela temperatura 1 sempre será um número entre 0 e 1, a subtração do número 1 por essa divisão será, também, um número entre 0 e 1. Portanto menor que a unidade, podendo assim ser escrito na forma de porcentagem.
Aqui, percebemos como a natureza age. Ela nos impossibilita de transformar toda energia cedida a um objeto em trabalho. Mas veja, isso parece ser bom, afinal aparece aqui a ideia de que os objetos absorvem energia e, como consequência, aumentam sua temperatura. Agora imagine a vida sem esse efeito? Imagine uma pessoa precisando de energia para se aquecer e não podendo? Por exemplo, dispor de uma fogueira para absorver essa energia necessária para aumentar sua temperatura? Parece que a coisa não é tão ruim assim, não é mesmo?
Observe que o ciclo de Carnot funciona entre duas isotermas e duas adiabáticas. Ok, não existe transformações isotérmicas no universo. Mas podemos fazer com que a transformação se aproxime o máximo possível de uma isoterma. Da mesma forma, não existe transformação adiabática na natureza, afinal todo os objetos estão emitindo e recebendo, nó mínimo, radiação Infravermelha. Assim, da mesma forma que na transformação isotérmica, podemos aproximar uma transformação o máximo possível de uma adiabática. Carnot nos mostra que se um engenheiro conseguir criar um motor que funcione o mais próximo possível da situação do seu ciclo, conhecido pelo seu nome, maior será o rendimento do mesmo. É isso que os engenheiros tentam fazer hoje. É por esse motivo que os motores de carros atuais têm rendimento muito superior aos do início do século passado.
Vamos a um exemplo:
Imaginemos uma máquina térmica que funciona entre duas fontes de temperaturas 400K e 600K. Esta máquina retira 200J da "fonte quente" e rejeita 160J para a "fonte fria". Vamos calcular o rendimento dessa máquina e o seu rendimento máximo.
Vamos calcular primeiro o rendimento da máquina:
Vemos que o rendimento dessa máquina é de 20%
Agora vamos calcular o rendimento máximo da máquina:
Vemos que o rendimento máximo dessa máquina, operando entre assas duas temperatura e funcionando sob o ciclo de Carnot, é de 33%.
Portanto, enfatizando, percebemos claramente que essa máquina térmica, que possui rendimento de 20%, poderá, operando no ciclo de Carnot, ter rendimento máximo de 33% e não mais do que isso. Logo, o engenheiro que trabalhasse no melhoramento dessa máquina, saberia que se ele empregasse seus esforços para melhorá-la, teria esse máximo de rendimento. Caso esse rendimento não o satisfizesse, ele desistiria dela e partiria para outra máquina que pudesse ter rendimento maior ou que fosse possível trabalhar entre duas fontes de diferença de temperatura maior.